本文为 雷锋字幕组 编译的技术博客,原标题Accelerating deep neural networks with tensor decompositions,作者为Jacob。
翻译 | 林立宏 整理 | 凡江
背景
在这篇文章中,我将引见几种低秩张量分解办法,用于在现有的深度学习模型中停止分层并使其更紧凑。我也将分享PyTorch代码,它运用 Tensorly 来停止在卷积层上的CP分解和Tucker分解。
虽然希望大局部帖子都是可以独立阅读的,关于张量分解的回忆可以在 这里 找到。Tensorly的作者也写了于Tensor的根底内容 十分棒的notebook 。这协助我很好的开端学习这块内容,建议你阅读一下这些内容。
加上裁剪(pruning),张量分解是放慢现有深度神经网络的适用工具,我希望这篇文章能让这些内容愈加容易了解。
这些办法需求将一个层分解成几个更小的层。虽然在分解后会有更多的层,但是浮点运算次数和权重的总数会变小。一些报告的后果是整个网络的x8倍的速度提升(不针对像imagenet这样的大型义务),或许imagenet中的特定层中x4倍的提升。我的结论是用这些分解方式,我可以取得x2到x4倍的减速,这取决于我情愿牺牲多少的精度。
在 这篇文章 中我引见了一些称为裁剪(pruning)的技术以增加模型中的参数数量。在一个数据集上正向传递(有时是反向传递)裁剪(pruning),然后依据网络中激活的一些规范对神经元停止排序。
完全不同的是,张量分解的方法只用到层的权重,假定网络层是参数化的,它的权重可以用一个矩阵或许是一个低秩的张量来表示。这意味这个它们在参数化的网络下效果最佳。像VGG神经网络设计为完全参数化的。另外一个关于参数化模型的例子是运用更少的类别对网络停止微调以完成更复杂的义务。
和裁剪(pruning)类似,分解之后经过模型需求微调来恢复精确性。
在我们会深化讨论细节之前,最初一件要阐明的事是,虽然这些办法是适用的,并给出了很好的后果,但它们有一些缺陷:
-
它们可以在一个线性权重上执行(比方一个卷积或许一个全衔接的层),疏忽了任何非线性的内容。
-
它们是贪心,自以为聪明地分解层,疏忽了不同层之间的互相作用。
目前还要试图处理这些成绩,而且它依然是一个活泼的研讨范畴。
截断SVD用于分解完全衔接的层
第一份我能找到的运用这个来减速深度神经网络的是在Fast-RNN论文中,Ross Girshick运用它来减速用于检测的全衔接层。代码可以在这里找到: pyfaster-rcnn implementation 。
SVD概略
奇特值分解使我们可以分解任何具有n行和m列的矩阵A:
S是一个对角矩阵,其对角线上有非负值(奇特值),并且通常被结构成奇特值按降序陈列的。U和V是正交矩阵:
假如我们取最大的奇特值并将其他的归零,我们失掉A的近似值:
具有作为Frobenius范数最接近于A的秩t矩阵的性质,所以假如t足够大,
是A的良好近似。
在全衔接层上的SVD
一个全衔接层通常是做了矩阵乘法,输出一个矩阵A然后添加一个偏向b:
我们可以取A的SVD,只保存第一个奇特值。
这不是一个完全衔接的层,而是指点我们如何完成它作为两个较小的:
-
第一个将有一个mxt的外形,将没有偏向,其权重将取自
。 -
第二个将有一个txn的外形,将有一个等于b的偏向,其权重将取自
。
权重总数从nxm下降到t(n + m)。
在卷积层上张量分解 在互联网思维的影响下,传统服务业不再局限于规模效益,加强对市场的反应速度成为传统服务业发展的首要选择。在互联网思维下,通过对传统服务业的改革,为传统服务业发展创造了全新的天地。
二维卷积层是一个多维矩阵(前面用-张量),有四个维度:
cols x rows x input_channels x output_channels.
遵照SVD的例子,我们想要以某种方式将张量分解成几个更小的张量。卷积层转换为几个较小近似的卷积层。
为此,我们将运用两种盛行的(至多在Tensor算法的世界中)张量分解:CP分解和Tucker分解(也称为高阶SVD或其他称号)。
1412.6553 运用微调CP分解减速卷积神经网络
1412.6553 Speeding-up Convolutional Neural Networks Using Fine-tuned CP-Decomposition 这篇论文阐明了假如CP分解可以用于卷积层的减速,正如我们会看到的,这将卷积层归入相似挪动网络的东西。
他们运用它来减速网络的速度,而不会分明降低精度。在我本人的实验中,我可以运用这个在基于VGG16的网络上取得x2减速,而不会降低精确度。
我运用这种办法的经历是,需求十分细心地选择学习率,微调以使其任务,学习率通常应该十分小(大约
)。
一个秩R矩阵可以被视为R秩和1矩阵的和,每个秩1矩阵是一个列向量乘以一个行向量:
SVD为我们提供了运用SVD中的U和V列来写矩阵和的办法:
假如我们选择一个小于矩阵满秩的R,那么这个和就是一个近似值,就像截断SVD的状况一样。
CP分解让我们推行了张量。
运用CP分解,我们的卷积核,一个四维张量公式,可以近似为一个选定的R:
我们希望R关于无效的分解是小的,但是对坚持近似高精度是足够大的。
带CP分解的卷积正向传递
为了传递图层,我们运用输出
停止卷积:
这给了我们一个方法来处理这个成绩:
1.首先做一个wise(1x1xS)与
卷积。这增加了从S到R输出通道的数量。下一步将在较多数量的通道上完成卷积,使其更快。
2.用
在空间维度上执行别离的卷积。
就像在
挪动网络
中一样,卷积是深度可分的,辨别在每个通道中完成。与mobilenets不同,卷积在空间维度上也是可分的
。
3.做另一个逐点卷积来改动从R到T的通道数量假如原始卷积层有一个偏向,在这一点上加上它。
留意像在挪动网中的逐点和深度卷积的组合。在运用mobilenets的时分,你必需从头开端训练一个网络来取得这个构造,在这里我们可以把现有的图层分解成这种方式。
与挪动网络一样,为了取得最快的速度,需求一个无效完成深度可别离卷积的平台。
用PyTorch和Tensorly卷积层CP分解

1511.06530 用于疾速和低功率挪动使用的深度卷积神经网络的紧缩
1511.06530 Compression of Deep Convolutional Neural Networks for Fast and Low Power Mobile Applications
这一篇十分酷的论文,阐明了如何运用Tucker分解来减速卷积层来失掉更好的后果。我也在基于VGG的参数化网络用了这种减速,比CP分解的精度要好。作者在论文中指出,它可以让我们运用更高的学习率(我用
)停止微调。
Tucker分解也称为高阶奇特值分解(HOSVD)或许其他称号,是对张量停止奇特值分解的一种推行。
它以为SVD的推行的缘由是
的重量通常是正交的,但这关于我们的目的并不重要。
被称为中心矩阵,并定义不同的轴如何互相作用。
在下面描绘的CP分解中,沿着空间维度
的分解招致空间上可别离的卷积。无论如何,过滤器是十分小的,通常是3x3或5x5,所以可别离的卷积并不节省我们少量的计算,而且是一个积极的近似。
Trucker分解有用的性质是,它不用沿着一切的轴(形式)分解。我们可以沿着输出和输入通道停止分解(形式2分解):
卷积正向传递与塔克分解
像CP分解一样,写一下卷积公式并拔出内核分解:
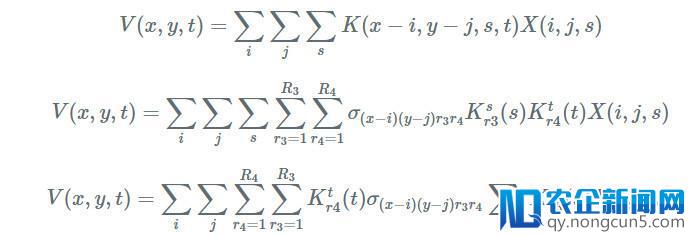
这给了我们以下用Tucker分解停止卷积的配方:
1.与
停止点对点卷积,信道从S增加到
的数量。
2.用
停止正则(不可分)卷积。这个卷积替代了原始层的S输出通道和T输入通道,具有
输出通道和
输入通道。假如这些等级小于S和T,这就是增加的缘由。
3.用
停止点对点卷积以回到原始卷积的T个输入通道。由于这是最初一次卷积,所以在这一点上,假如有偏向就加上偏向。
我们如何选择分解行列
一种办法是尝试不同的值并反省精确性。尝试后的启示是
,效果很好。
理想状况下,选择行列应该是自动的。
作者提出运用 变分贝叶斯矩阵分解(VBMF)(Nakajima等,2013) 作为估量等级的办法。
VBMF很复杂,不在本文的讨论范围内,但是在一个十分高层次的总结中,他们所做的是将矩阵
近似为低秩矩阵
和高斯噪声之和。在找到A和B之后,H是等级的下限。
为了将其用于Tucker分解,我们可以展开原始权重张量的s和t重量来创立矩阵。然后我们可以运用VBMF估量
和
作为矩阵的秩。
我用这个 在Python上完成的VBMF ,置信它可以任务。
VBMF通常前往的秩,十分接近我之前,细心和有趣的手动调整失掉的后果。
这也可以用于估量完全衔接层的截断SVD减速的等级。
用PyTorch和Tensorly卷积层Tucker分解

总结
在这篇文章中,我们讨论了几个张量分解的办法来减速深度神经网络。
-
截断的SVD可用于减速完全衔接的层。
-
CP分解将卷积层分解成相似挪动网络的东西,虽然它更具侵略性,由于它在空间维度上也是可分的。
-
Tucker分解增加了二维卷积层操作的输出和输入通道的数量,并且运用逐点卷积来切换2D卷积之前和之后的通道数量。
我觉得风趣的是网络设计中的罕见形式,逐点和深度卷积,自但是然呈现在这些分解中!
博客旧址 https://jacobgil.github.io/deeplearning/tensor-decompositions-deep-learning
更多文章,关注雷锋网
(大众号:雷锋网)
,添加
雷锋字幕组
微信号(leiphonefansub)为好友
备注「我要参加」,To be a AI Volunteer !

雷锋网雷锋网
。

