雷锋网 (大众号：雷锋网) AI 科技评论按：ICLR 2018  于 5 月初在加拿大温哥华举行。论文「Efficient Sparse-Winograd Convolutional Neural Networks」被 ICLR 2018 录用，第一作者、斯坦福大学的博士生刘星昱为雷锋网AI 科技评论撰写了独家解读稿件，未经答应不得转载。

引言

卷积神经网络在许多机器学习使用中表现出宏大优势。其计算功能和功耗次要由卷积进程中乘法操作的数量决议。但卷积神经网络的宏大计算量限制了其在挪动设备上的使用。

目前有两种主流办法用于增加卷积神经网络中的乘法数量：

• 1）应用卷积的线性代数性质，例如 Winograd 卷积算法可以经过神经元和卷积核的线性变换增加乘法数量；

• 2）神经网络紧缩，例如应用权重经过剪枝后的稀疏性和神经元由于 ReLU 发生的稀疏性。

但是，上述两个方向无法兼容：对神经元和卷积核的线性变换会使得它们本来的稀疏性不复存在，因而无法应用其稀疏性停止减速。在稀疏卷积神经网络上运用 Winograd 卷积算法会反而使计算量增大。

针对上述成绩，本文提出两点改良。

• 首先，我们将 ReLU 激活函数移至 Winograd 域，使得在乘法操作时神经元是稀疏的；

• 其次，我们对 Winograd 变换之后的权重停止剪枝，使得在乘法操作时权重是稀疏的。

实验后果标明，在精度损失 0.1% 之内时，我们提出的新办法在 CIFAR-10，CIFAR-100 和 ImageNet 数据集上能将乘法数量辨别增加 10.4 倍，6.8 倍和 10.8 倍，乘法增加率相较于原有基准提升 2.0-3.0 倍。

稀疏 Winograd 卷积

传统 Winograd 卷积算法的根本单元作用在输出时域特征图 d 的大小为 p x p 的小块上，经过 3 x 3 的时域卷积核 g 卷积失掉 (p-2) x (p-2) 的输入块 S。一切的输入块拼在一同失掉输入特征图。

详细操作： d 和 g 辨别用矩阵 B 和 G 停止变换失掉 Winograd 域的 p x p 大小的 B^TdB 和 GgG^T，两者停止 Hadamard 乘法后用矩阵 A 停止变换失掉 S。当 p 等于 4 时，矩阵 B 和 A 只含有 0，1 和-1 元素，因而与 B 和 A 的乘法只需求加减法。计算进程如下公式所示： 

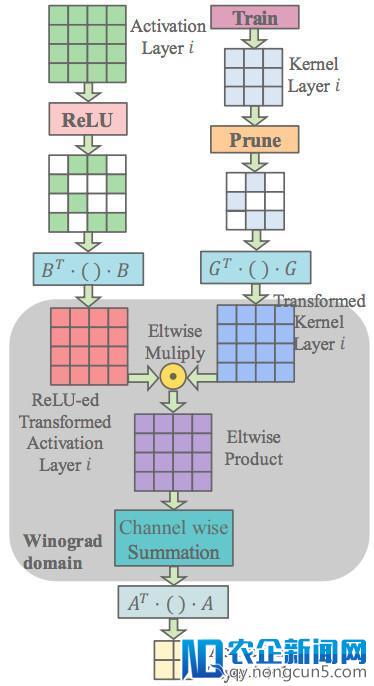
时域剪枝网络： 当运用普通剪枝的网络 (Han et al. 2015) 时，前一层的 ReLU 激活函数作用在时域输出 d 上，同时时域权重 g 被剪枝。输入块 S 由以下对于互联网金融P2P企业来说，支付市场完善的标准和管理系统将彻底改变互联网金融行业的格局，不仅给从业者提供了的巨大的发展机遇，也带来了全新的挑战。公式计算失掉：

当 p=4 时的计算如下图所示。虽然 d 和 g 辨别由于 ReLU 和剪枝都是稀疏的，但是 G(•)G^T 和 B^T(•)B 变换会抹掉时域的 0。因而，稀疏性无法增加乘法数量。

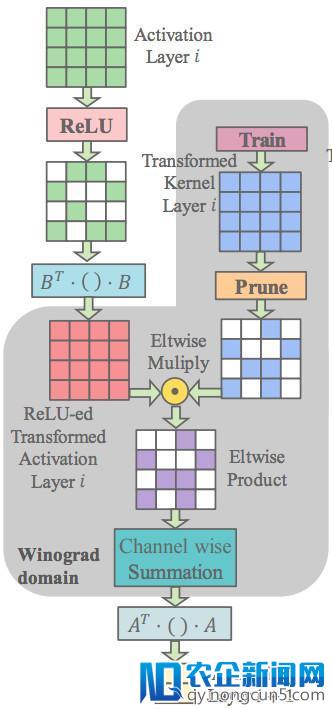
Winograd 本地剪枝网络： 当运用 Winograd 本地剪枝网络 (Liu et al. 2017, Li et al. 2017) 时，前一层的 ReLU 激活函数作用在时域输出 d 上，同时 Winograd 域权重 GgG^T 被剪枝。输入块 S 由以下公式计算失掉 

当 p=4 时的计算如下图所示。虽然由于剪枝，Winograd 域的权重 GgG^T 是稀疏的，但是 B^T(•)B 变换会抹掉时域 d 中包括的 0。因而，时域 d 由于 ReLU 形成的稀疏性依然无法带来乘法数量增加。

 

Winograd-ReLU 卷积神经网络： 为理解决上述成绩，我们提出了 Winograd-ReLU 卷积神经网络。我们将 ReLU 操作放在 Winograd 域而不是时域。如此，在停止乘法操作时，Winograd 域的权重 GgG^T 和输出 B^TdB 都是稀疏的，乘法数量得以进一步增加。输入块 S 由以下公式计算失掉

 

当 p=4 时的计算如下图所示。

 

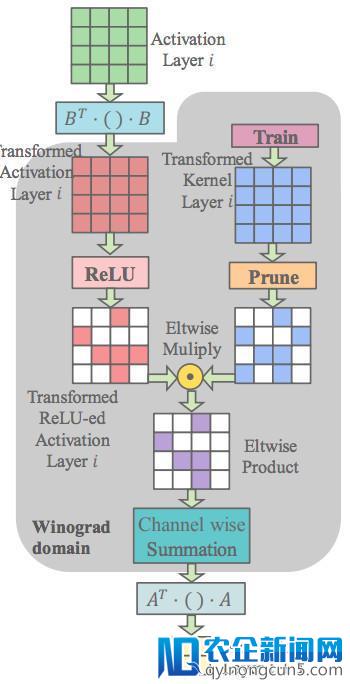
值得留意的是，我们完全抛弃了时域的卷积核。由于 ReLU 是和前一层的卷积层绑定的，Winograd 域的 ReLU 操作实践上是从第二层开端的。需求指出，新提出的卷积神经网络架构和普通的卷积神经网络在数学上不等价。因而，网络的训练、剪枝和重训练都需求停止如下改动。

训练： 我们直接在 Winograd 域训练变换后的卷积核。卷积核随机初始化后直接由反向传达计算梯度停止优化。

剪枝： 我们对 Winograd 域卷积核停止剪枝：一切相对值小于阈值 t 的元素置为 0。阈值 t 是经过到达某一要求的剪枝率 r 计算失掉的。在我们停止的实验中，一切层的剪枝率是相反的。

重训练： 我们应用前一步失掉的剪枝掩码来停止重训练。在重训练进程中，被剪枝的权重经过掩码强迫设置为 0。网络损失函数对输出神经元和 Winograd 域权重的梯度可经过链式规律由下游传递来的梯度计算失掉：

实验和后果

我们将上述办法使用在不同数据集上的不同网络架构上。我们选择实验的网络架构中大少数卷积核的大小为 3x3，这可以保证大少数卷积层都可以转化为 Winograd 卷积层。我们辨别运用图像分类数据集 CIFAR-10、CIFAR-100 和 ImageNet 停止实验。对每个网络架构我们比拟前述三类网络。三类网络都是从头开端训练并停止迭代的剪枝-重训练进程。

CIFAR-10：

我们运用 VGG-nagadomi 网络停止实验。VGG-nagadomi 可以视作轻量级的 VGGNet，其中有 8 层 3x3 卷积层。我们将第一层的权重密度设为 80%，其他层迭代地从 80% 剪枝为 20%。

 

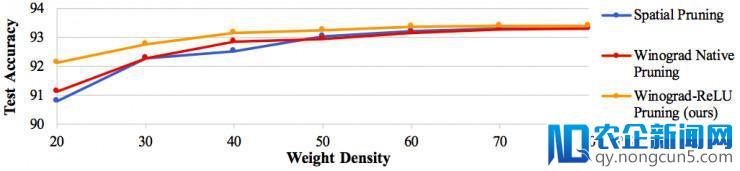
由上图可以看到，当精确率损失小于 0.1% 时，时域剪枝网络、Winograd 本地剪枝网络仅可以被剪枝到 60% 密度，而我们提出的 Winograd-ReLU 网络可以被剪枝到 40% 密度。  

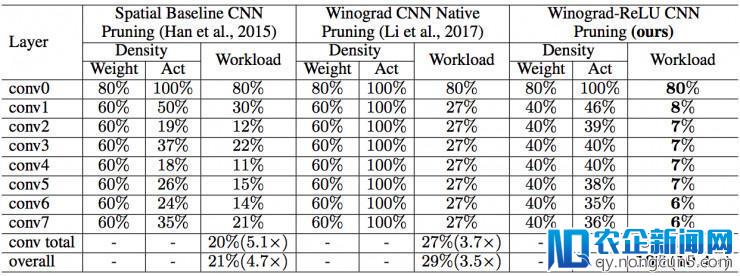
上表比拟了各个剪枝后网络的计算量以及权重和输出神经元的密度。时域剪枝网络、Winograd 本地剪枝网络仅可以将计算量辨别增加 5.1 和 3.7 倍。而我们提出的 Winograd-ReLU 网络可以增加计算量 13.3 倍，相较于两个基准网络辨别提升 2.6 和 3.6 倍。

CIFAR-100：

我们运用 ConvPool-CNN-C 网络停止实验。ConvPool-CNN-C 有 9 个卷积层，其中有 7 个 3x3 卷积层。我们将第一层的权重密度设为 80%，其他层迭代地从 80% 剪枝为 20%。

 

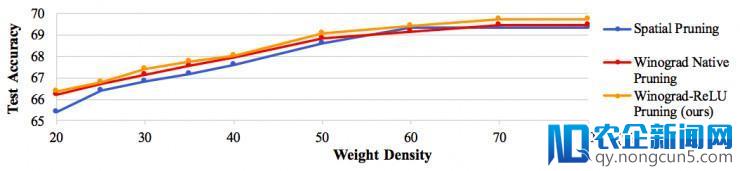
由上图可以看到，当精确率损失小于 0.1% 时，Winograd 本地剪枝网络可以被剪枝到 70% 密度，而时域剪枝网络和我们提出的 Winograd-ReLU 网络可以被剪枝到 60% 密度。

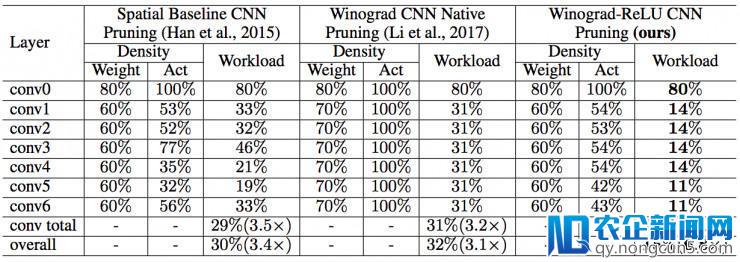
上表比拟了各个剪枝后网络的计算量以及权重和输出神经元的密度。时域剪枝网络、Winograd 本地剪枝网络仅可以将计算量辨别增加 3.5 和 3.2 倍。而我们提出的 Winograd-ReLU 网络可以增加计算量 7.1 倍，相较于两个基准网络辨别提升 2.1 和 2.2 倍。

ImageNet：

我们运用 ResNet-18 网络的一个变体停止实验。该变体与原 ResNet-18 的差异在于，我们用 1x1 步长 3x3 卷积以及 2x2 池化层来替代 2x2 步长 3x3 卷积。同时我们也去掉了最初一个池化层，使得最初一组卷积层的大小为 14x14。我们将卷积层的权重密度迭代地从 80% 剪枝为 10%。

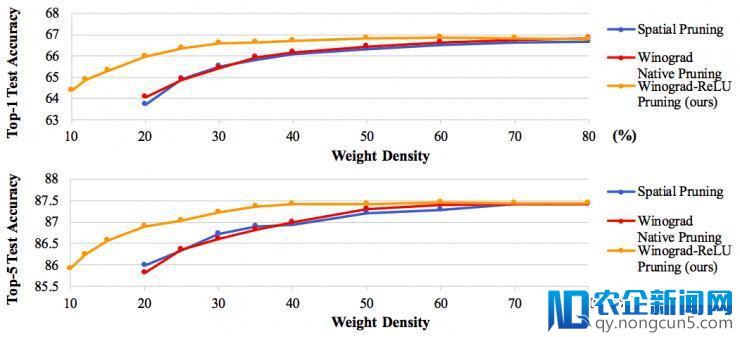
由上图可以看到，当精确率损失小于 0.1% 时，时域剪枝网络、Winograd 本地剪枝网络仅可以被辨别剪枝到 60% 和 50% 密度，而我们提出的 Winograd-ReLU 网络可以被剪枝到 30%/35% 密度。

 

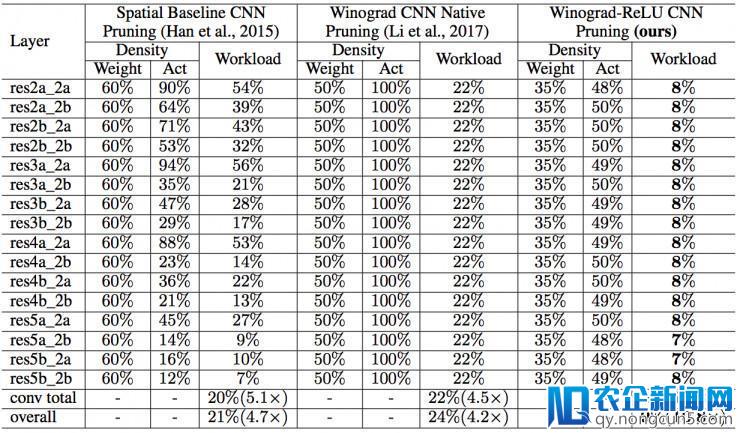
上表比拟了各个剪枝后网络的计算量以及权重和输出神经元的密度。时域剪枝网络、Winograd 本地剪枝网络仅可以将计算量辨别增加 5.1 和 4.5 倍。而我们提出的 Winograd-ReLU 网络可以增加计算量 13.2 倍，相较于两个基准网络辨别提升 2.6 和 2.9 倍。

讨论

我们对提出的 Winograd-ReLU 网络的卷积核停止可视化。我们挑选了 res2a_2a 层的前 6 个输出和输入通道。可以看到，Winograd-ReLU 网络的卷积核并未显示出分明的物理意义。但是，我们发现 (2,2) 元素（从左至右从上至下，初始目标为 1）通常较其它元素更明显。一个能够的缘由在于，(2,2) 元素在 Winograd 域输出神经元中是特别的：它是 B^TdB 中独一一个只由加法而无减法停止线性变换的神经元。在润滑的输出特征图中，这意味着 (2,2) 元素是独一拥有非零均值的元素。

。
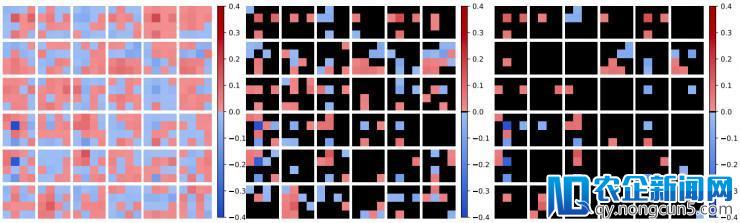