近期，我们在生活中常常会听到关于机器学习与人工智能（AI）方面的信息。机器正学着模拟人类大脑，自动处置各类任务。可以自动驾驶的车辆则在学习理解驾驶路况，还有可以与人类对话的公家助手，以及像人类一样预测股票市场走势的机器等。从某些方面来说，机器学习几乎像“魔法”一样神奇。

但在机器学习的面前，使用了许多根底性、深化研讨过的技术。人类需求学习如何应用这些技术来处理某类成绩。首先需求理解一下这些技术，再来阐明发现存在不当拜访非构造化数据成绩时的处理方案。

机器学习——定义：

机器学习属于人工智能，计算机可以应用训练或察看学习到的算法来探测相关形式并确定其基准行为。机器学习可以处置与剖析海量数据，这关于人类来说可不是轻而易举的事情。

机器学习义务次要分为两大类：

1、监视学习：向机器内输出各种材料，以及预期输入内容，如此，当前只需录入相关内容，就能得出预期输入。

2、无监视学习：此类机器用于在没有明白输出详细查询形式的前提下，检测数据集中的各类数据形式。

更重要的是，在无监视机器学习进程中，有多种技术可辨认各类数据形式，最终生成有价值的剖析构造。理解成绩域是正确的选择使用技术的关键。数据专家们的次要义务之一就是要确定该运用哪种技术。如数据专家不理解成绩域，则无法选择正确的办法处理成绩。

聚类：

聚类是向同类组分配对象的进程（亦称为簇），旨在确保各组的对象都不同。聚类属于无监视义务，用于描绘对象的隐藏构造。

各对象由一系列特点组成，称之为特征。划分对象到不同集群时，首先要确定各个对象间的间隔。定义适当间隔测量法是成功完成聚类的关键。

k-means：

目前有许多聚类算法可用，各有优缺陷。常用的聚类算法就是 k-means，这种算法可以迭代法辨认出最佳的k 聚类中心。聚类中心是与聚类相关的对象“代表”，k-means的次要优缺陷如下：

1、必需明白指定聚类数量，但某些状况下无法晓得各类聚类的数量；

2、k-means的迭代特性容易因部分最小值会聚发生错误后果。

3、假定聚类是球状的。

虽然有这些缺陷，但在许多状况下，k-means仍是最正确也是最常用的算法。关于球面数据运用k-means的聚类示例可见图1。

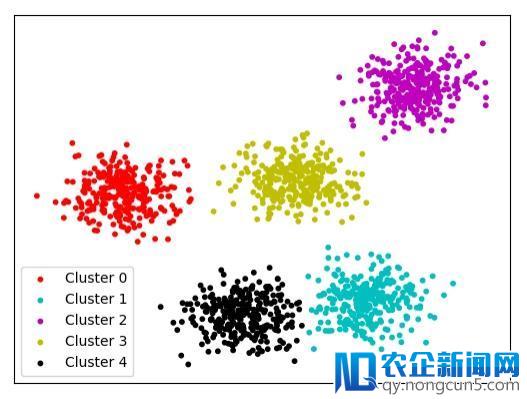
图1：球状数据上的k-means聚类

OPTICS 聚类算法：

另外一种聚类算法是OPTICS，它是基于密度的聚类算法。基于密度的聚类算法，与基于质心的聚类算法不同，这种算法经过辨认点簇“密度”，理解恣意外形与密度的聚类。OPTICS还可经过辨认出分散的对象来确定数据的离群值（噪声）。

图2： k-means与OPTICS使用于数据时的比照

OPTICS与k-means算法会生成一模一样的数据点组；它会将离群值分类，并更为准确的按数据性质而非球状的方式来表现簇。可参见图2在数据上使用k-means及OPTICS后的比照示例。

降维：

在机器学习范畴，通常针对高维数据采用降维法处置。此处置办法旨在增加需求思索的各类特征数据，由于每项特征都代表了对象的一个局部。

为何降维如此重要？随着特征的增多，数据变的愈加稀疏，因而需求从维度灾难方面停止剖析。此外，还便于处置小型数据集。

应用以下两个办法执行降维：

1、从现有特征中选择（特征选择）

2、组合现有特征后，提取新特征（特征提取）。

特性提取的次要技术是主成份剖析法（PCA）。主成份剖析法可保证找到最佳线性变换，降低维数数量，增加信息损失。有时，丧失的信息被称为噪声，这种信息并不具有代表性，只是局部未知顺序的反作用而已。主成份剖析法的视觉表达如下（图3）：

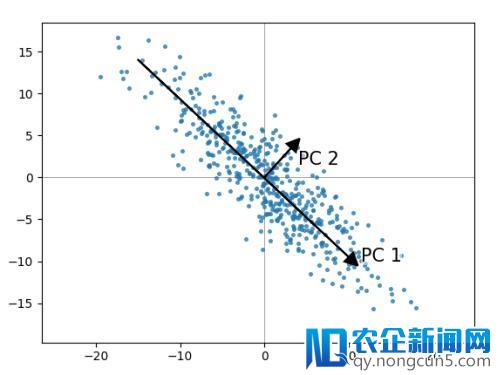
图3：主成份剖析法

上述示例中，能够对PC1的后果表示称心，最终以一个特性取代了原来的两个特性。

有许多降维技术可选择：局部线性技术，如：主成份剖析法，局部非线性技术以及前期日趋普遍运用的深度学习法等（词嵌入）。

将相关技术用于静态学习对等组：

Imperva Defense Center近期的黑客情报方案（HII）调查报告中提到了文件平安的最新创新办法。这种办法会应用无监视机器静态学习对等组。一旦学会了对等组，就可以用对等组来确定每个用户拜访组织中的各种共享文档的虚拟权限能否正确。Imperva的违规进攻处理方案CounterBreach中就运用了这种静态对等组功用。

图4引见了如何依据静态对等组剖析后果，应用机器学习探测可疑文件拜访活动。

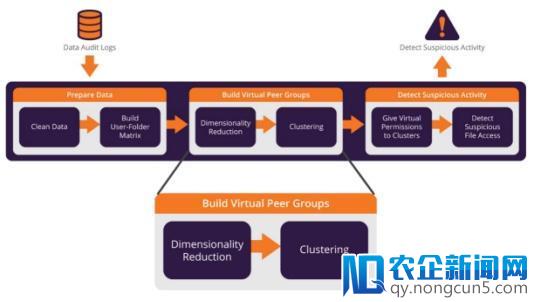
图4：应用静态对等组剖析后果探测可疑活动的进程

首先Imperva将审计数据转化为用户拜访目录的矩阵，其中横坐标为用户与纵坐标为文件夹。矩阵单元内的值为指定用户拜访文件夹的活动量。然后，Imperva会停止降维的处置。运用PCA的首个缘由就是矩阵的稀疏性，由于矩阵单元内99%以上都是空的。其次，许多文件夹的拜访形式都是关联的，从而招致矩阵呈现多重共线性。而实践上在我们的案例中，多组用户会在一个相似项目中任务，这些用户都有关联性，因而被放置在相似的文件夹组中。最初，运用PCA后，矩阵范围减少了90%，因而更便于处置。搜集与预备数据后，机器学习可构建虚拟对等组。Imperva应用前述机器学习技术（即：PCA以及基于密度的聚集法）构建静态对等组。

其次，Imperva选择OPTICS算法作为其聚集算法，即：依据密度来聚集用户。由于对等组数据未知，而k-means需求理解簇的数量——本案中为需求理解对等组数量，因而无法运用该算法。

OPTICS则不受此数据限制。OPTICS还便于采取特殊手腕处置噪声用户，即：将噪声用户独自放入一个簇内。除上述缘由外，经过少量的实验与辨错后，确认OPTICS是本数据集最佳算法。

小结：

选择正确的算法是数据剖析三要素最重要的一个环节。数据剖析三要素：首先就是数据自身，其次是数据预备任务，即：清算与选择可以代表数据特点的详细特征，第三就是应用正确的机器学习法，适当描绘数据。

本案中，PCA与OPTICS都是经过证明，特别适用于学习对等任务组的工具。但“机器”并不能神奇的自我决策。只要人（也就是团队）才干理解成绩所在，剖析数据，并“魔法般的”选择正确的机器学习法构建人工智能的高楼大厦。