雷锋网 (大众号:雷锋网) AI 研习社按:本文为雷锋网字幕组编译的技术博客,原文章标题为:How to build your own Neural Network from scratch in Python,作者 James Loy
原文链接: https://towardsdatascience.com/how-to-build-your-own-neural-network-from-scratch-in-python-68998a08e4f6
翻译 | 刘彩虹 周辉 校正 | 于志鹏 整理 | 孔令双
动机 :为了愈加深化的了解深度学习,我们将运用 python 言语从头搭建一个神经网络,而不是运用像 Tensorflow 那样的封装好的框架。我以为了解神经网络的外部任务原理,对数据迷信家来说至关重要。
这篇文章的内容是我的所学,希望也能对你有所协助。
神经网络是什么?
引见神经网络的文章大少数都会将它和大脑停止类比。假如你没有深化研讨过大脑与神经网络的类比,那么将神经网络解释为一种将给定输出映射为希冀输入的数学关系会更容易了解。
神经网络包括以下组成局部
-
一个输出层,x
-
恣意数量的隐藏层
-
一个输入层,ŷ
-
每层之间有一组权值和偏置,W and b
-
为隐藏层选择一种激活函数,σ。在教程中我们运用 Sigmoid 激活函数
下图展现了 2 层神经网络的构造(留意:我们在计算网络层数时通常扫除输出层)
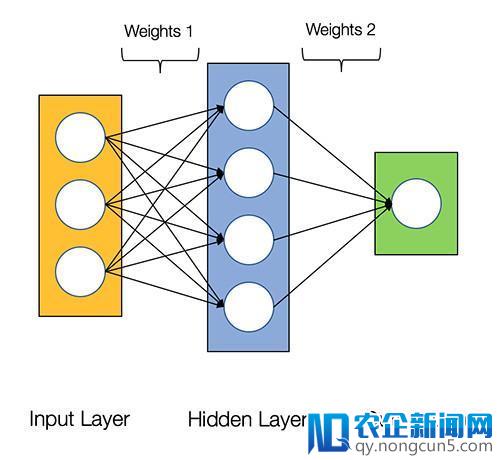
2 层神经网络的构造
用 Python 可以很容易的构建神经网络类
class NeuralNetwork:
def __init__(self, x, y):
self.input = x
self.weights1 = np.random.rand(self.input.shape[1],4)
self.weights2 = np.random.rand(4,1)
self.y = y
self.output = np.zeros(y.shape)
训练神经网络
这个网络的输入 ŷ 为:
你能够会留意到,在下面的等式中,输入 ŷ 是 W 和 b 函数。
因而 W 和 b 的值影响预测的精确率. 所以依据输出数据对 W 和 b 调优的进程就被成为训练神经网络。
每步训练迭代包括以下两个局部:
-
计算预测后果 ŷ,这一步称为前向传达
-
更新 W 和 b,,这一步成为反向传达
上面的顺序图展现了这个进程:

前向传达
正如我们在上图中看到的,前向传达只是复杂的计算。关于一个根本的 2 层网络来说,它的输入是这样的:
我们在 NeuralNetwork 类中添加一个计算前向传达的函数。为了复杂起见我们假定偏置 b 为0:
class NeuralNetwork:
def __init__(self, x, y):
self.input = x
self.weights1 = np.random.rand(self.input.shape[1],4)
self.weights2 = np.random.rand(4,1)
self.y = y
self.output = np.zeros(self.y.shape)
def feedforward(self):
self.layer1 = sigmoid(np.dot(self.input, self.weights1))
self.output = sigmoid(np.dot(self.layer1, self.weights2))
但是我们还需求一个办法来评价预测后果的好坏(即预测值和真实值的误差)。这就要用到损失函数。
损失函数
常用的损失函数有很多种,依据模型的需求来选择。在本教程中,我们运用误差平方和作为损失函数。
误差平方和是求每个预测值和真实值之间的误差再求和,这个误差是他们的差值求平方以便我们察看误差的相对值。
训练的目的是找到一组 W 和 b,使得损失函数最好小,也即预测值和真实值之间的间隔最小。
反向传达
我们曾经度量出了预测的误差(损失),如今需求找到一种办法来传达误差,并以此更新权值和偏置。
为了晓得如何适当的调整权值和偏置,我们需求晓得损失函数对权值 W 和偏置 b 的导数。
回想微积分中的概念,函数的导数就是函数的斜率。
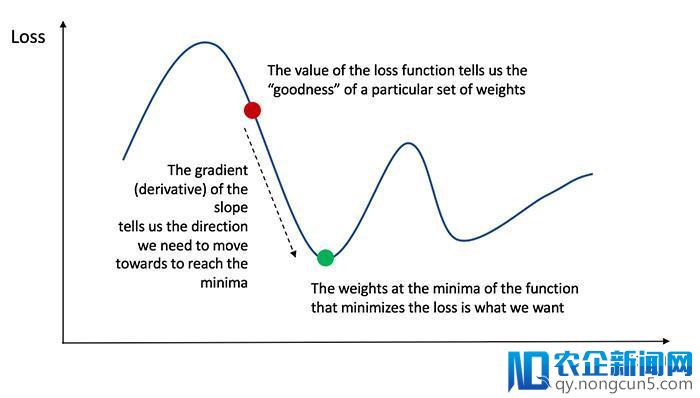
梯度下降法
假如我们曾经求出了导数,我们就可以经过添加或增加导数值来更新权值 W 和偏置 b(参考上图)。这种方式被称为 梯度下降法 。
但是我们不能直接计算损失函数对权值和偏置的导数,由于在损失函数的等式中并没有显式的包括他们。因而,我们需求运用链式求导发在来协助计算导数。
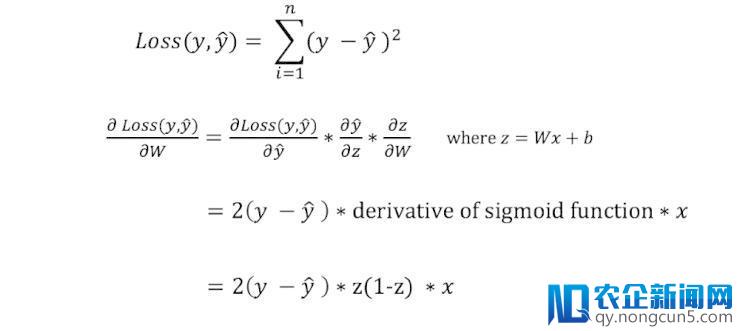
链式规律用于计算损失函数对 W 和 b 的导数。留意,为了复杂起见。我们只展现了假定网络只要 1 层的偏导数。
这虽然很粗陋,但是我们仍然能失掉想要的后果—损失函数对权值 W 的导数(斜率),因而我们可以相应的调整权值。
如今我们将反向传达算法的函数添加到 Python 代码中
class NeuralNetwork:
def __init__(self, x, y):
self.input = x
self.weights1 = np.random.rand(self.input.shape[1],4)
self.weights2 = np.random.rand(4,1)
self.y = y
self.output = np.zeros(self.y.shape)
def feedforward(self):
self.layer1 = sigmoid(np.dot(self.input, self.weights1))
self.output = sigmoid(np.dot(self.layer1, self.weights2))
def backprop(self):
# application of the chain rule to find derivative of the loss function with respect to weights2 and weights1
d_weights2 = np.dot(self.layer1.T, (2*(self.y - self.output) * sigmoid_derivative(self.output)))
d_weights1 = np.dot(self.input.T, (np.dot(2*(self.y - self.output) * sigmoid_derivative(self.output), self.weights2.T) * sigmoid_derivative(self.layer1)))
# update the weights with the derivative (slope) of the loss function
self.weights1 += d_weights1
self.weights2 += d_weights2
为了更深化的了解微积分原理和反向传达中的链式求导规律,我激烈引荐 3Blue1Brown 的如下教程:
Youtube: https://youtu.be/tIeHLnjs5U8
整兼并完成一个实例
既然我们曾经有了包括前向传达和反向传达的完好 Python 代码,那么就将其使用到一个例子上看看它是如何任务的吧。
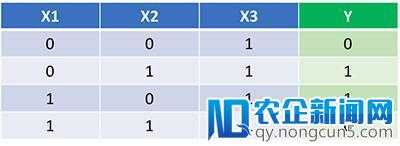
神经网络可以经过学习失掉函数的权重。而我们仅靠察看是不太能够失掉函数的权重的。
让我们训练神经网络停止 1500 次迭代,看看会发作什么。 留意察看上面每次迭代的损失函数,我们可以清楚地看到损失函数单调递加到最小值。这与我们之前引见的梯度下降法分歧。
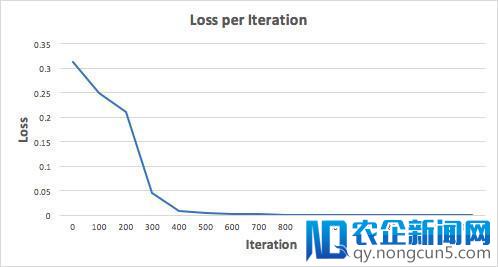
让我们看看经过 1500 次迭代后的神经网络的最终预测后果:
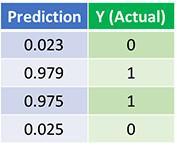
经过 1500 次迭代训练后的预测后果
我们成功了!我们使用前向和方向传达算法成功的训练了神经网络并且预测后果收敛于真实值。
留意预测值和真实值之间存在纤细的误差是允许的。这样可以避免模型过拟兼并且使得神经网络关于未知数据有着更强的泛化才能。
下一步是什么?
侥幸的是我们的学习之旅还没有完毕,依然有很多关于神经网络和深度学习的内容需求学习。例如:
-
除了 Sigmoid 以外,还可以用哪些激活函数
-
在训练网络的时分使用学习率
-
在面对图像分类义务的时分运用卷积神经网络
我很快会写更多关于这个主题的内容,敬请等待!
最初的想法
我本人也从零开端写了很多神经网络的代码
虽然可以运用诸如 Tensorflow 和 Keras 这样的深度学习框架方便的搭建深层网络而不需求完全了解其外部任务原理。但是我觉得关于有追求的数据迷信家来说,了解外部原理是十分无益的。
这种练习对我本人来说已成成为重要的工夫投入,希望也能对你有所协助。
文章首发于雷锋网 AI 研习社(okweiwu)。
。
