本文为 雷锋字幕组 编译的技术博客，原标题The 5 Clustering Algorithms Data Scientists Need to Know，作者为George Seif。

翻译 | 姜波    整理 |  凡江  吴璇

聚类是一种关于数据点分组的机器学习技术。给出一组数据点，我们可以运用聚类算法将每个数据点分类到特定的组中。实际上，同一组中的数据点应具有类似的属性或特征，而不同组中的数据点应具有相当不同的属性或特征（即类内差别小，类间差别大）。聚类是一种无监视学习办法，也是一种统计数据剖析的常用技术，被普遍使用于众多范畴。

在数据迷信中，我们可以经过聚类算法，检查数据点属于哪些组，并且从这些数据中取得一些有价值的信息。明天，我们一同来看看数据迷信家需求理解的5种盛行聚类算法以及它们的优缺陷。

一、K均值聚类

K-Means能够是最知名的聚类算法了。在数据迷信或机器学习课程中都有过它的引见。K-Means的代码也十分容易了解和完成。请检查上面的图片：

 

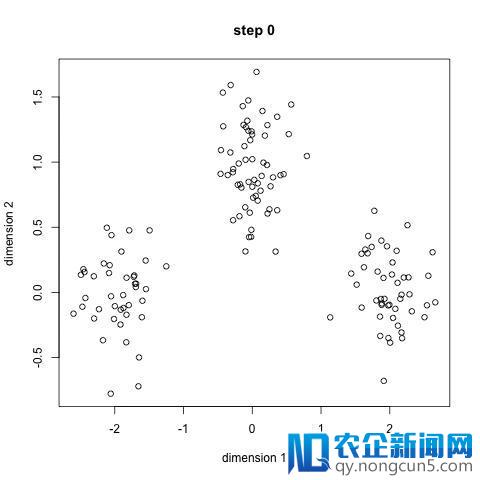
1. 开端，我们先选取一些类型或许组类，辨别随机初始化它们的中心点。要计算出运用的类的数量，最好疾速检查数据并尝试辨认不同的分组。中心点是与每个数据点向量长度相反的向量，并且是上图中的‘X’s’。

2. 每一个数据点，是经过计算该点与每一组中的点之间的间隔，来停止分类的，然后将该点归类到间隔中心最近的组。

3. 基于这些分类的点，我们经过求取每一组中一切向量的均值，反复计算每一组的中心点。

4. 反复上述步骤，直到每一组的中心点不再发作变化或许变化不大为止。你也可以选择对组中心点停止屡次随机初始化，选择运转效果最好的即可。

5. 由于我们所做的只是计算点和组中心之间的间隔，计算量较小，因而K-Means的一大优点就是运转速度十分快。所以它具有线性复杂度O(n）。

当然，K-Means也有两个缺陷。首先，你必需选择有分类组的数目（如聚为3类，则K=3）。这并不能疏忽，理想状况下，我们希望它运用聚类算法来协助我们了解这些数据，由于它的重点在于从数据中取得一些有价值的发现。由于K-means算法选择的聚类中心是随机的（即初始化是随机的），因而它能够会由于类数不同而运转算法中发生不同的聚类后果。因而，后果能够不可反复且缺乏分歧性。相反，其他集群办法更分歧。

K-Medians是与K-Means有关的另一种聚类算法，不同之处在于我们运用组的中值向量来重新计算组中心点。该办法对异常值不敏感（由于运用中值），但关于较大的数据集运转速度就要慢得多，由于在计算中值向量时，需求在每次迭代时停止排序。

二、Mean-Shift聚类

均匀移位聚类是基于滑动窗口的算法，试图找到密集的数据点区域。这是一种基于质心的算法，意味着目的是定位每个组/类的中心点，经过更新中心点的候选点作为滑动窗口内点的均匀值来任务。然后在后处置（绝对‘预处置’来说的）阶段对这些候选窗口停止滤波以消弭近似反复，构成最终的中心点集及其相应的组。请检查上面的图片：

 

Mean-Shift聚类用于单个滑动窗口

1. 为理解释均匀偏移，我们将思索像上图那样的二维空间中的一组点。我们从以C点（随机选择）为中心并以半径r为中心的圆滑动窗口开端。均匀偏移是一种爬山算法，它触及将这个核迭代地转移到每个步骤中更高密度的区域，直到收敛。

2. 在每次迭代中，经过将中心点挪动到窗口内的点的均匀值（因而得名），将滑动窗口移向较高密度的区域。滑动窗口内的密度与其外部的点数成反比。当然，经过转换到窗口中的点的均匀值，它将逐步走向更高点密度的区域。

3. 我们持续依据均匀值挪动滑动窗口，直到没无方向移位可以在内核中包容更多点。看看下面的图片;我们持续挪动该圆，直到我们不再添加密度（即窗口中的点数）。

4. 步骤1至3的这个进程用许多滑动窗口完成，直到一切点位于一个窗口内。当多个滑动窗口堆叠时，保存包括最多点的窗口。数据点然后依据它们所在的滑动窗口聚类。

上面显示了一切滑动窗口从头到尾的整个进程的阐明。每个黑点代表滑动窗口的质心，每个灰点代表一个数据点。

Mean-Shift聚类的整个进程

与K均值聚类相比，不需求选择聚类数量，由于均值偏移可以自动发现。这是一个宏大的优势。聚类中心向最大密度点聚合的后果也是十分令人称心的，由于它的了解比拟契合数据驱动的规律，且非常直观。缺陷是窗口大小/半径r的选择是十分重要的，换句话说半径的选择决议了运转后果。

三、基于密度的噪声使用空间聚类（DBSCAN）

DBSCAN是一种基于密度的聚类算法，相似于mean-shift，但其拥有一些显着的优点。 看看上面的另一个花哨的图形，让我们开端吧！

 

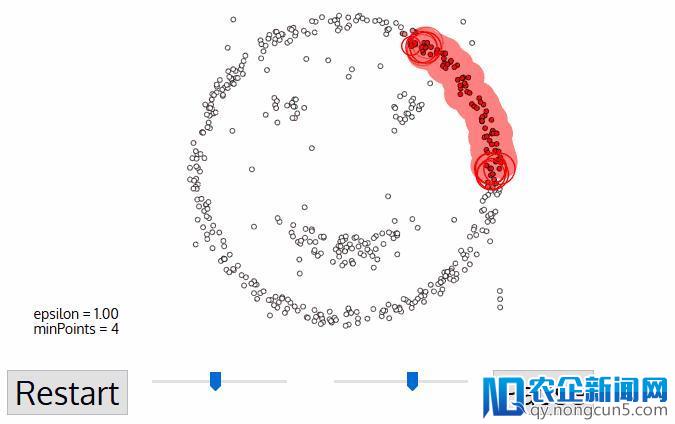
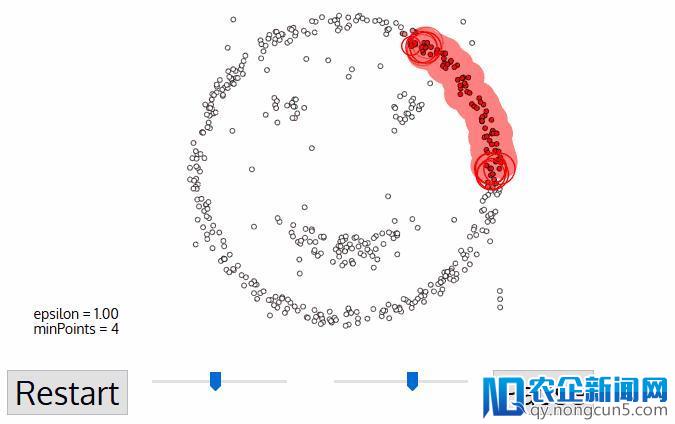
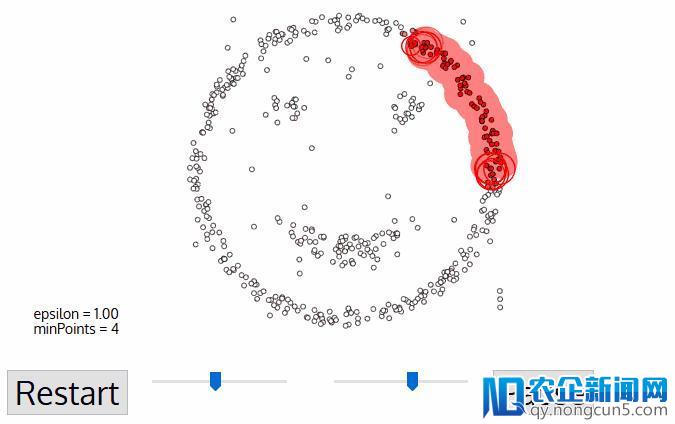
1. DBSCAN以任何尚未拜访过的恣意起始数据点开端。这个点的邻域用间隔epsilon提取（ε间隔内的一切点都是邻域点）。

2. 假如在该邻域内有足够数量的点（依据minPoints），则聚类进程将开端并且以后数据点将成为新聚类中的第一个点。否则，该点将被标志为噪声（稍后，这个噪声点能够会成为群集的一局部）。在这两种状况下，该点都被标志为“已拜访”。

3. 关于新簇中的第一个点，ε间隔邻域内的点也成为同一个簇的一局部。然后对曾经添加到群集组中的一切新点反复使ε邻域中的一切点属于同一个群集的进程。

4. 反复步骤2和3的这个进程直到聚类中的一切点都被确定，即聚类的ε邻域内的一切点都被拜访和标志。

5. 一旦我们完成了以后的集群，一个新的未拜访点被检索和处置，招致发现更多的集群或噪声。反复此进程，直到一切点都被标志为已拜访。由于一切点曾经被拜访终了，每个点都被标志为属于一个簇或是噪声。

6. 与其他聚类算法相比，DBSCAN具有一些很大的优势。 首先，它基本不需求pe-set数量的簇。 它还将异常值辨认为噪声，而不像mean-shift，即便数据点十分不同，它们也会将它们引入群集中。 另外，它可以很好地找就任意大小和恣意外形的簇。

DBSCAN的次要缺陷是，当簇的密度不同时，DBSCAN的功能不如其他组织。 这是由于当密度变化时，用于辨认临近点的间隔阈值ε和minPoints的设置将随着群集而变化。 关于十分高维的数据也会呈现这种缺陷，由于间隔阈值ε再次难以估量。

四、运用高斯混合模型（GMM）的希冀最大化（EM）聚类

K-Means的次要缺陷之一是其运用了集群中心的均匀值。 经过检查上面的图片，我们可以明白为什么这不是选取聚类中心的最佳方式。 在左侧，人眼看起来十分分明的是，有两个半径不同的圆形星团以相反的均匀值为中心。K-Means无法处置这个成绩，由于这些集群的均匀值十分接近。K-Means在集群不是圆形的状况下也会出错，这也是由于运用均值作为集群中心的缘由。

 

K-Means的两个失败案例

高斯混合模型（GMMs）比K-Means更具灵敏性。关于GMM，我们假定数据点是高斯散布的。这是一个限制较少的假定，而不是用均值来表示它们是循环的。这样，我们有两个参数来描绘群集的外形，均值和规范差。以二维数据为例，这意味着群集可以采取任何类型的椭圆形（由于我们在x和y方向都有规范偏向）。 因而，每个高斯散布被分配给单个集群。

为了找到每个群集的高斯参数（例如均匀值和规范偏向），我们将运用希冀最大化（EM）的优化算法。 看看上面的图表，作为合适群集的高斯图的例证。然后我们可以持续停止运用GMM的希冀最大化聚类进程

 

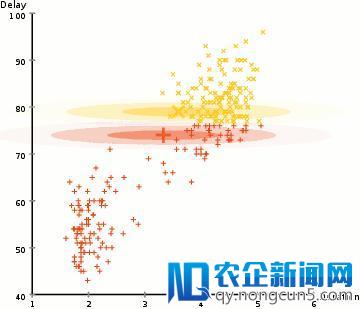
运用GMM的EM聚类

1. 我们首先选择簇的数量（如K-Means）并随机初始化每个簇的高斯散布参数。人们可以尝试经过疾速检查数据来为初始参数提供良好的假定。请留意，这不是100％必要的，由于开端时高斯散布化十分弱，虽然从上图可以看出，但随着算法的运转很快就能失掉优化。

2. 给定每个群集的这些高斯散布，计算每个数据点属于特定群集的概率。一个点越接近高斯中心，它越能够属于该群。这应该是直观的，由于关于高斯散布，我们假定大局部数据更接近集群的中移动互联网在带来全新社交体验的同时，也或多或少使人们产生了依赖。移动互联网使网络、智能终端、数字技术等新技术得到整合，建立了新的产业生态链，催生全新文化产业形态。心。

3. 基于这些概率，我们为高斯散布计算一组新的参数，以便使集群内数据点的概率最大化。我们运用数据点地位的加权和来计算这些新参数，其中权重是属于该特定群集中的数据点的概率。为了以可视化的方式解释这一点，我们可以看看下面的图片，特别是黄色的群集。散布从第一次迭代开端随机开端，但我们可以看到大局部黄点都在该散布的右侧。当我们计算一个按概率加权的和时，即便中心左近有一些点，它们中的大局部都在左边。因而，分配的均值自然会更接近这些点的集合。我们也可以看到，大局部要点都是“从右上到左下”。因而，规范偏向改动以创立更合适这些点的椭圆，以便最大化由概率加权的总和。

4. 步骤2和3迭代地反复直到收敛，其中散布从迭代到迭代的变化不大。

运用GMM有两个关键优势。首先GMM比K-Means在群协方面更灵敏。由于规范偏向参数，集群可以采取任何椭圆外形，而不是限于圆形。K均值实践上是GMM的一个特例，其中每个群的协方差在一切维上都接近0。其次，由于GMM运用概率，每个数据点可以有多个群。因而，假如一个数据点位于两个堆叠的簇的两头，我们可以复杂地定义它的类，将其归类为类1的概率为百分之x，类2的概率为百分之y。

五、凝聚层次聚类

分层聚类算法实践上分为两类：自上而下或自下而上。自下而上算法首先将每个数据点视为单个群集，然后延续兼并（或聚合）成对的群集，直到一切群集兼并成包括一切数据点的单个群集。自下而上的层次聚类因而被称为分层凝聚聚类或HAC。该簇的层次构造被表示为树（或树状图）。树的根是搜集一切样本的独一聚类，叶是仅有一个样本的聚类。在进入算法步骤之前，请检查上面的图解。

 

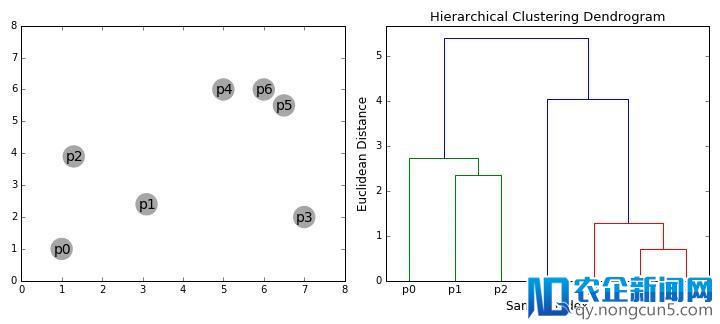
凝聚层次聚类

1. 我们首先将每个数据点视为一个单一的聚类，即假如我们的数据集中有X个数据点，则我们有X个聚类。然后我们选择一个度量两个集群之间间隔的间隔度量。作为一个例子，我们将运用均匀关联，它将两个集群之间的间隔定义为第一个集群中的数据点与第二个集群中的数据点之间的均匀间隔。

2. 在每次迭代中，我们将两个群集兼并成一个群集。将要组合的两个群被选为均匀联络最小的群。即依据我们选择的间隔度量，这两个群集之间的间隔最小，因而是最类似的，应该结合起来。

3. 反复步骤2直到我们抵达树的根部，即我们只要一个包括一切数据点的聚类。经过这种方式，我们可以最终选择我们想要的簇数量，只需选择何时中止组合簇，即中止构建树。

分层聚类不需求我们指定聚类的数量，我们甚至可以选择哪个数量的聚类看起来最好，由于我们正在构建一棵树。另外，该算法对间隔度量的选择不敏感;他们都倾向于任务异样好，而与其他聚类算法，间隔度量的选择是至关重要的。分层聚类办法的一个特别好的用例是根底数据具有层次构造并且您想要恢复层次构造;其他聚类算法无法做到这一点。与K-Means和GMM的线性复杂性不同，这种层次聚类的优点是以较低的效率为代价，由于它具有O（n3）的工夫复杂度。

结论

数据迷信家应该晓得的这5个聚类算法！我们将等待一些其他的算法的执行状况以及可视化，敬请等待Scikit Learn！

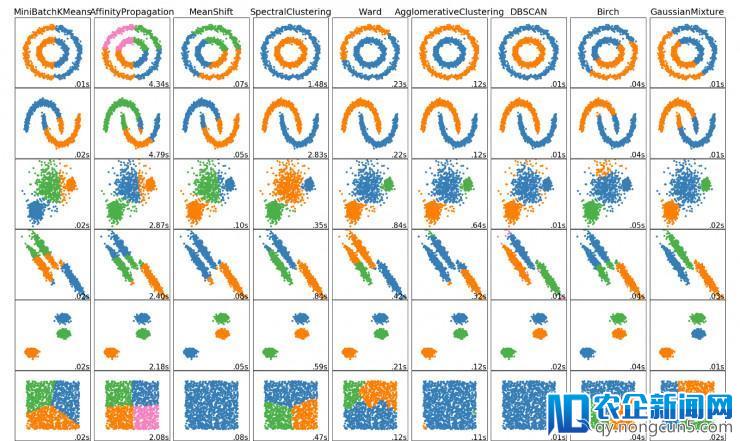
博客旧址 https://towardsdatascience.com/the-5-clustering-algorithms-data-scientists-need-to-know-a36d136ef68

---

更多文章，关注雷锋网 (大众号：雷锋网)

添加 雷锋字幕组 微信号（leiphonefansub）为好友

备注「我要参加」，To be an  AI  Volunteer ！

雷锋网雷锋网

相关文章：

如何成为一名数据迷信家？Yann LeCun 的建议也许能给你答案

。