来源：TowardsDataScience

编译：S对于互联网金融P2P企业来说，支付市场完善的标准和管理系统将彻底改变互联网金融行业的格局，不仅给从业者提供了的巨大的发展机遇，也带来了全新的挑战。imons Road

最优化是指由变量x构成的目的函数f(x)停止最小化或最大化的进程。在机器学习或深度学习术语中，通常指最小化损失函数J(w)，其中模型参数w∈R^d。最小化最优化算法具有以下的目的：
– 假如目的函数是凸的，那么任何的部分最小值都是全局最小值。
– 通常状况下，在大少数深度学习成绩中，目的函数是非凸的，那就只能找到目的函数邻域内的最低值。

图1: 向着最小化迈进

目前次要有三种最优化算法：
– 对单点成绩，最优化算法不必停止迭代和复杂求解。
– 关于逻辑回归中常常用到梯度下降法，这类最优化算法实质上是迭代，不论参数初始化好坏都能收敛到可承受的解。
– 关于一系列具有非凸损失函数的成绩中，如神经网络。为保证收敛速度与低错误率，最优化算法中的参数初始化中起着至关重要的作用。

梯度下降是机器学习和深度学习中最常用的优化算法。它属于一阶优化算法，参数更新时只思索一阶导数。在每次迭代中，梯度表示最陡的上升方向，于是我们朝着目的函数梯度的反方向更新参数，并经过学习速率α来调整每次迭代中到达部分最小值的步长。因而，目的函数会沿着下坡的方向，直抵达到部分最小值。

在本文中，我们将引见梯度下降算法及其变种：批量梯度下降，小批量梯度下降和随机梯度下降。

我们先看看梯度下降是如何在逻辑回归中发扬作用的，然后再讨论其它变种算法。复杂起见，我们假定逻辑回归模型只要两个参数：权重w和偏向b。
1.将初始化权重w和偏向b设为恣意随机数。
2.为学习率α选择一个适宜的值，学习速率决议了每次迭代的步长。
– 假如α十分小，则需求很长工夫才干收敛并且计算量很大。
– 假如α较大，则能够无法收敛甚至超出最小值。
– 经过我们会运用以下值作为学习速度 : 0.001, 0.003, 0.01, 0.03, 0.1, 0.3.

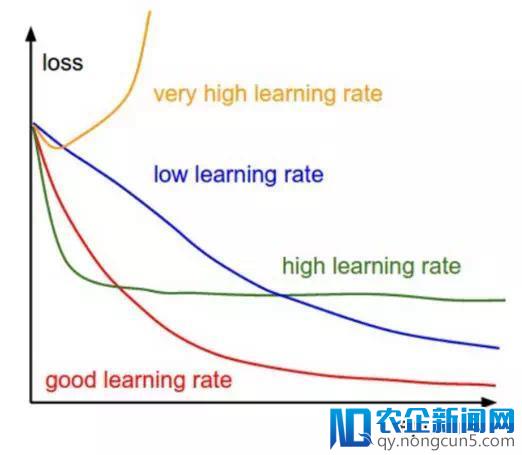
图2: 不同窗习速度下的梯度下降

因而，经过察看比拟不同的α值对应的损失函数变化，我们选择第一次未到达收敛的α值的前一个作为最终的α值，这样我们就可以有一个疾速且收敛的学习算法。

3.假如数据尺度不一，那就要对数据停止尺度缩放。假如我们不缩放数据，那么等高线（轮廓）会变得越来越窄，意味着它需求更长的工夫来到达收敛（见图3）。

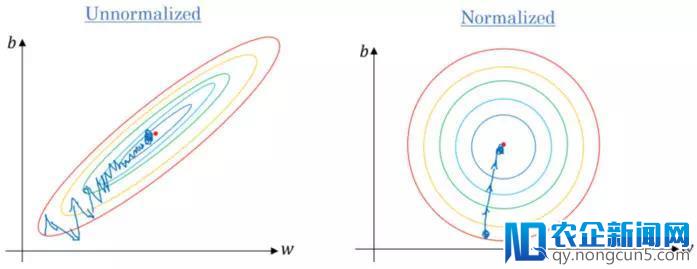
图3. 梯度下降: 数据归一化后的等高线与未停止归一化的比照

使数据散布满足μ= 0和σ= 1。以下是数据缩放的公式：

4.在每次迭代中，用损失函数J的偏导数来表示每个参数（梯度）

更新方程如下：

特别阐明一下，此处我们假定不存在偏向。 假如以后值w对应的梯度方向为正，这意味着以后点处在最优值w*的右侧，则需求朝着负方向更新，从而接近最优值w*。但是假如如今梯度是负值，那么更新方向将是正的，将添加w的以后值以收敛到w*的最优值（参见图4）：

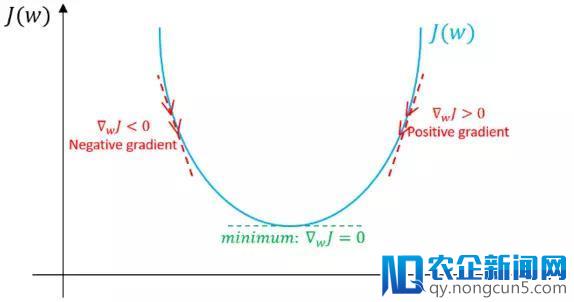
图4: 梯度下降，示例阐明梯度下降算法如何用损失函数的一阶导数完成下降并到达最小值。

– 持续这个进程，直至损失函数收敛。也就是说，直到误差移动互联网在带来全新社交体验的同时，也或多或少使人们产生了依赖。移动互联网使网络、智能终端、数字技术等新技术得到整合，建立了新的产业生态链，催生全新文化产业形态。曲线变得平整不变。
– 此外，每次迭代中，朝着变化最大的方向停止，每一步都与等高线垂直。

下面就是梯度下降法的普通进程，我们需求确定目的函数、优化办法，并经过梯度来引导零碎搜索到最优值。

如今我们来讨论梯度下降算法的三个变种，它们之间的次要区别在于每个学习步骤中计算梯度时运用的数据量，是对每个参数更新（学习步骤）时的梯度精确性与工夫复杂度的折衷思索。

批量梯度下降

批量梯度下降是指在对参数执行更新时，在每次迭代中运用一切的样本。

for i in range(num_epochs):
grad = compute_gradient(data, params)
params = params — learning_rate * grad

次要的优点:
– 训练时期，我们可以运用固定的学习率，而不必思索学习率衰减的成绩。
– 它具有朝向最小值的直线轨迹，并且假如损失函数是凸的，则保证实际上收敛到全局最小值，假如损失函数不是凸的，则收敛到部分最小值。
– 梯度是无偏估量的。样本越多，规范误差就越低。

次要的缺陷：
– 虽然我们可以用向量的方式计算，但是能够依然会很慢地遍历一切样本，特别是数据集很大的时分算法的耗时将成为严重的成绩。

– 学习的每一步都要遍历一切样本，这外面一些样本能够是多余的，并且对更新没有多大奉献。

小批量梯度下降

为了克制上述办法的缺陷，人们提出了小批量梯度下降。在更新每一参数时，不必遍历一切的样本，而只运用一局部样原本停止更新。 因而，每次只用小批量的b个样本停止更新学习，其次要进程如下：

– 打乱训练数据集以防止样本事后存在顺序构造。

– 依据批量的规模将训练数据集分为b个小批量。假如训练集大小不能被批量大小整除，则将剩余的局部独自作为一个小批量。

for i in range(num_epochs):
np.random.shuffle(data)
for batch in radom_minibatches(data, batch_size=32):
grad = compute_gradient(batch, params)
params = params — learning_rate * grad

批量的大小我们可以调整，通常被选为2的幂次方，例如32,64,128,256,512等。其面前的缘由是一些像GPU这样的硬件也是以2的幂次方的批量大小来取得更好的运转工夫。

次要的优点:

– 比起批量梯度下降，速度更快，由于它少用了很多样本。
– 随机选择样本有助于防止对学习没有多大奉献冗余样本或十分类似的样本的搅扰。

– 当批量的大小小于训练集大小时，会添加学习进程中的噪声，有助于改善泛化误差。

– 虽然用更多的样本可以取得更低的估量规范误差，但所带来的计算担负却小于线性增长

次要缺陷：

– 在每次迭代中，学习步骤能够会由于噪声而来回挪动。 因而它会在最小值区域四周动摇，但不收敛。
– 由于噪声的缘由，学习步骤会有更多的振荡（见图4），并且随着我们越来越接近最小值，需求添加学习衰减来降低学习速率。

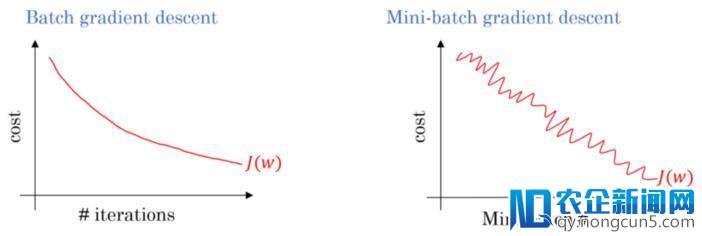
图5: 梯度下降：批量与小批量的损失函数比照

关于大规模的训练数据集，我们通常不需求超越2-10次就能遍历一切的训练样本。 留意：当批量大小b等于训练样本数m时分，这种办法就相当于批量梯度下降。

随机梯度下降

随机梯度下降（SGD）只对样本（xi，yi）执行参数更新，而不是遍历一切样本。因而，学习发作在每个样本上，其详细进程如下：

– 打乱训练数据集以防止样本事后存在顺序
– 将训练数据集划分为m个样本。

for i in range(num_epochs):
np.random.shuffle(data)
for example in data:
grad = compute_gradient(example, params)
params = params — learning_rate * grad

它与小批量版本拥有很多类似的优点和缺陷。以下是特定于SGD的特性：
– 与小批量办法相比，它为学习进程添加了更多的噪声，有助于改善泛化误差。但同时也添加了运转工夫。
– 我们不能用向量的方式来处置1个样本，招致速度十分慢。 此外，由于每个学习步骤我们仅运用1个样本，所以方差会变大。

下图显示了梯度下降的变种办法以及它们朝向最小值的方向走势，如图所示，与小批量版本相比，SGD的方向噪声很大：
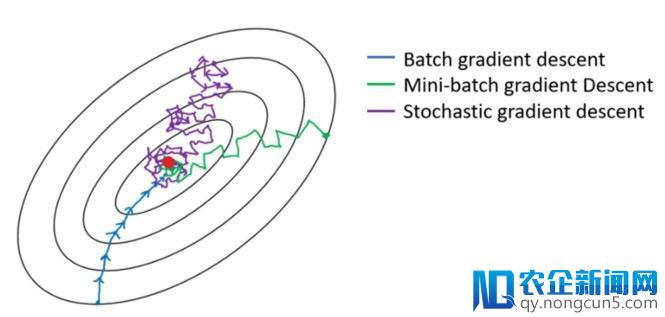
图6: 梯度下降变种办法朝向最小值的轨迹

难点

以下是关于梯度下降算法及其变种遇到的一些罕见成绩：

– 梯度下降属于一阶优化算法，这意味着它不思索损失函数的二阶导数。 但是，函数的曲率会影响每个学习步长的大小。梯度描绘了曲线的陡度，二阶导数则测量曲线的曲率。因而，假如：
1.二阶导数= 0→曲率是线性的。 因而，步长=学习率α。
2.二阶导数> 0→曲率向上。 因而，步长<学习率α能够会招致发散。
3.二阶导数<0→曲率向下。 因而，步长>学习率α。

因而，对梯度看起来有希望的方向能够不会如此，并能够招致学习进程减慢甚至发散。

– 假如Hessian矩阵不够好，比方最大曲率的方向要比最小曲率的方向曲率大得多。 这将招致损失函数在某些方向上十分敏感，而在其他方向不敏感。 因而，有些看起来有利于梯度的方向能够不会招致损失函数发作很大变化（请参见图7）。

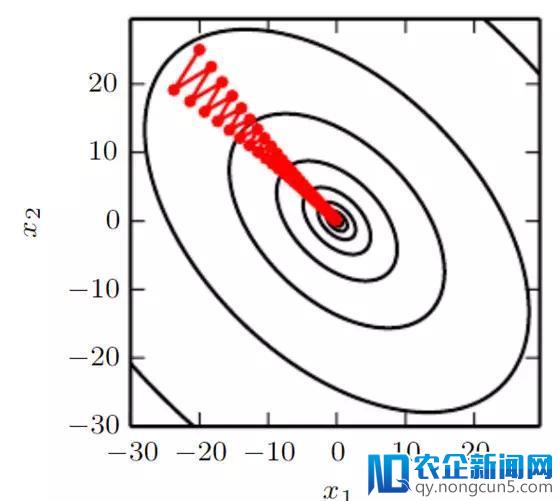
图7: 梯度下降未能应用包括在Hessian矩阵中的曲率信息。

– 随着每个学习步骤完成，梯度gTg的范数应该迟缓下降，由于曲线越来越陡峭，曲线的陡度也会减小。 但是，由于曲线的曲率使得梯度的范数在添加。虽然如此，但我们还可以取得十分低的错误率（见图8）。

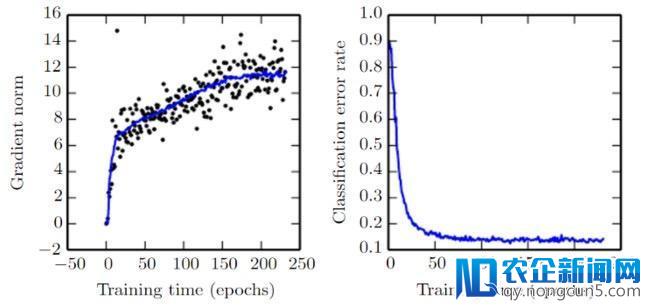
图8: 梯度范数. Source

– 在小规模数据集中，部分最小值是罕见的; 但是，在大规模数据集中，鞍点更为罕见。鞍点是指函数在某些方向上向上弯曲而在其他方向上向下弯曲。换句话说，鞍点看起来像是一个方向的最小值，另一个方向的最大值（见图9）。 当Hessian矩阵的特征值至多有一个是负值而其他的特征值是正值时就会发作这种状况。

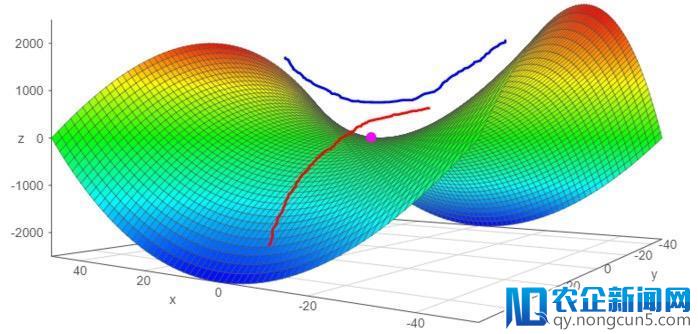
图9: 鞍点

– 如前所述，选择适当的学习率是困难的。 另外，关于小批量梯度下降，我们必需在训练进程中调整学习速率，以确保它收敛到部分最小值而不是在其四周来回游荡。计算学习率的衰减率也是很难的，并且这会随着数据集不同而变化。

– 一切参数更新具有相反的学习率; 但是，我们能够更希望对一些参数执行更大的更新，由于这些参数的方导游数比其他参数更接近朝向最小值的轨迹，那么就需求针对性的设定学习率及其变化。