大众号/将门创投

来源：TowardsDataScience

编译：Simon’s Road

模型的好坏和优劣 都是基于一定的角度做出的绝对判别，在这篇文章中，我们将从目的和成绩的角度去讨论每种误差度量的无效性。 当有人通知你“中国是最好的国度”时，你问的首要成绩一定是这个陈说的根底是什么，我们是依据国度的经济情况、文明程度还是他们的卫生设备等来评价比拟各个国度的呢？ 相似地，每个机器学习模型都用到了不同的数据集来有针对性的处理不同目的的成绩，因而，在选择适宜的度量之前，要深入了解上下文。

 

图 各种机器学习模型常用的度量规范

回归度量目标

大少数的博客更多都关注模型的精度、召回率、AUC(Area under curve，ROC曲线下区域面积)等分类目标。这里想稍稍改动一下，让我们来探究各种更多的目标，包括在回归成绩中运用的目标。MAE和RMSE是关于延续变量的两个最普遍的度量规范。

首先，我们看看最盛行RMSE，全称是Root Mean Square Error，即均方根误差，它表示预测值和观测值之间差别（称为残差）的样本规范偏向。在数学上，它是用如下这个公式计算的：

 

其次是MAE，全称是Mean Absolute Error，即均匀相对误差，它表示预测值和观测值之间相对误差的均匀值。MAE是一种线性分数，一切集体差别在均匀值上的权重都相等，比方，10和0之间的相对误差是5和0之间相对误差的两倍。但这关于RMSE而言不一样，后续将进一步详细讨论。在数学上，MAE是用如下这个公式计算的：

那么你应该选择哪一个？为什么这样选择呢？

首先，了解和解释MAE很容易，由于它就是对残差直接计算均匀，而RMSE相比MAE，会对高的差别惩罚更多。让我们经过两个例子来了解一下：

案例1：真实值= [2,4,6,8]，预测值= [4,6,8,10]

案例2：真实值= [2,4,6,8]，预测值= [4,6,8,12]

案例1的MAE = 2.0，RMSE = 2.0

案例2的MAE = 2.5，RMSE = 2.65

从上述例子中，我们可以发现RMSE比MAE愈加多地惩罚了最初一项预测值。通常，RMSE要大于或等于MAE。等于MAE的独一状况是一切残差都*相等或都为零*，如案例1中一切的预测值与真实值之间的残差皆为2，那么MAE和RMSE值就相等。

> 虽然RMSE更复杂且倾向更高的误差，它依然是许多模型的默许度量规范，由于用RMSE来定义损失函数是*平滑可微*的，且更容易停止数学运算。

虽然这听起来不太令人称心，但这确实是是它十分受欢送的缘由。上面我将从数学角度解释上述逻辑。首先，让我们树立一个复杂的单变量线性模型：y = mx + b，在这个成绩中，我们要找到最佳“m”和“b”，数据（x，y）是已知的。假如我们用RMSE来定义损失函数（J）：那么我们可以很容易地求得J对m和b的偏导，并以此来更新m和b（这是梯度下降的任务方式，这里就不过多解释它）

上述等式很容易就可以求解，但对MAE并不适用。但是，假如你需求一种度量规范能从直观解释的角度来比拟两个模型，那么我以为MAE会是更好的选择。值得留意的是，RMSE和MAE的单位与y值相反，但R Square不是这样的。此外，RMSE和MAE的范围都是从0到无量大。

> 这里需求提及MAE和RMSE之间的一大重要区别，最小化一组数字的平方误差会失掉其均匀值，而最小化相对误差则会失掉其中值， 这也是为什么MAE比RMSE对离群点更无效的缘由。

R Squared, R² 校正 R Squared

R² 和校正R²，经常用于阐明选择的自变量对解释因变量解释拟合有多好。

在数学上，R_Squared由下式给出：

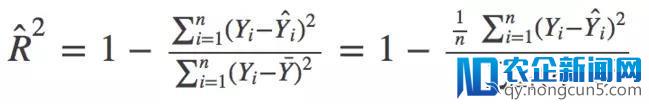
> 其中，分子是MSE（残差平方的均匀值），分母是Y值的方差。MSE越高，R_squared则越小，标明模型越差。

跟R²一样，校正R²也显示了自变量对因变量的解释水平，回归成绩中表现于曲线的拟合优度，但是可以依据模型中的自变量个数停止调整。 它由以下公式给出：

其中n表示观测值的总数，k表示预测值的数量，校正后的R²总是小于或等于R²。

为什么你应该越过R²选择校正R²？

规范的R²在运用中往往会存在一些成绩，但运用校正R²就能很好地处理。由于校正R²会思索在模型中添加附加项，使得功能改善。假如你添加有用的项，R²会添加，而假如添加了不太有用的预测变量，R²将增加。 但是，即便模型没有实践改良，R²也随着变量数量的添加而添加。上面我们用一个例子来更好天文解这一点。

这里，案例1是一个很复杂的状况，我们有5个察看值（x，y）。 在案例2中，让一个变量是变量1的两倍（也就是说它与变量1完全相关）。在案例3中，我们对变量2做了细微的搅扰，使其不再与变量1完全相关。

因而，假如我们为每个案例都用复杂普通的最小二乘（OLS）模型来拟合，那么从逻辑上讲，我们为案例1、案例2和案例3提供的信息是相反的，那我们的度量值绝对这些模型也不会有所进步。但是，实践上R² 关于模型2和3会给出更高的值，这显然是不正确的。但是，用校正R²就可以处理这个成绩，实践上关于案例2和3都是增加的。让我们给这些变量（x ，y）赋上一些值，并检查Python中取得的后果。

留意：模型1和模型2的预测值将相反，因而R²也将相反，由于它仅取决于预测值和实践值。

从上表可以看出，从案例1到案例3，虽然我们没有添加的任何附加信息，但R²仍在添加，而校正后的R²显示了正确的趋向（惩罚模型2拥有更多的变量）

比照校正R²与RMSE

关于后面的例子，我们将看到案例1和案例2失掉的RMSE后果与R²是相似的。在这种状况下，校正R²要比RMSE更好，由于它只对预测值与实践值停止比拟。而且，RMSE的相对值实践上并不能阐明模型有多蹩脚，它只能用于比拟两个模型，但校正R²就很容易做到这一点。 例如，假如一个模型的如今R²为0.05，那么这个模型一定很差。

但是，假如你只关怀预测精度，那么RMSE是最佳选择。它计算复杂，容易区分，普通是大少数模型的默许度量。

罕见误区：我常常看到网上说R²的范围在0到1之间，实践上并不是这样。R²的最大值是1，但最小值可以是负无量大。即便y的真实值为负数，模型对一切观测值的预测后果也会有高负值的状况。在这种状况下，R²将小于0。这虽然是一个不太能够的状况，但能够性仍然存在。

风趣的目标

这里有一个风趣的目标，假如你对NLP感兴味，Andrew Ng在深度学习课程中引见了它。 BLEU（Bilingual evaluation Understudy，双语评价研讨）

它次要用于权衡机器翻译绝对于人类翻译的质量，它运用了准确度量的修正方式。

计算BLEU分数的步骤:

1. 把句子转换成单个词、两个词、三个词和四个词

2. 辨别计算大小为1至4的n语法的精度

3. 取一切这些精度值的加权均匀的指数

4.将其与冗长的惩罚项相乘（稍后将解释）

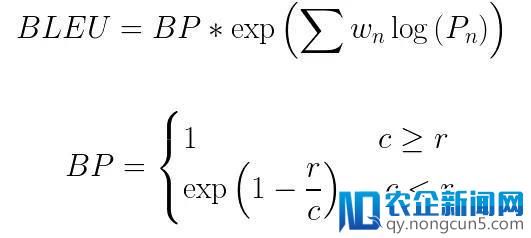
这里BP是冗长的惩罚项，r和c辨别是参考翻译和候选翻译中的词的数量，w 表示权重，P表示精度值

例：

参考：The cat is sitting on the mat

机器翻译1：On the mat is a cat

机器翻译2：There is cat sitting cat

我们来比拟一下下面两个翻译的BLEU得分。

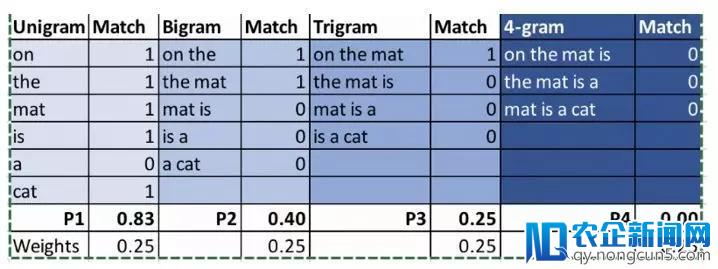
最终后果：BLEU（MT1）= 0.454，BLEU（MT2）= 0.59

为什么要引入简约的惩罚项？

引入的惩罚项会惩罚那些短于参考翻译的候选翻译。例如，假如上述候选翻译的参考翻译是“The cat”，那么它关于单个词和两个词将具有很高的精度，由于两个单词都以相反的顺序呈现在参考翻译中。但是，长度太短的话，实践上并不能很好的反映参考翻译的含义。有了这个冗长的惩罚，候选翻译必需在长度、相反单词和单词顺序方面与参考翻译相婚配才干取得高分。

希望经过这篇文章的引见，我们能了解不同度量间的差别，并能为机器学习选择适宜的模型度量，评价建模效果的好坏，并指点模型的优化。